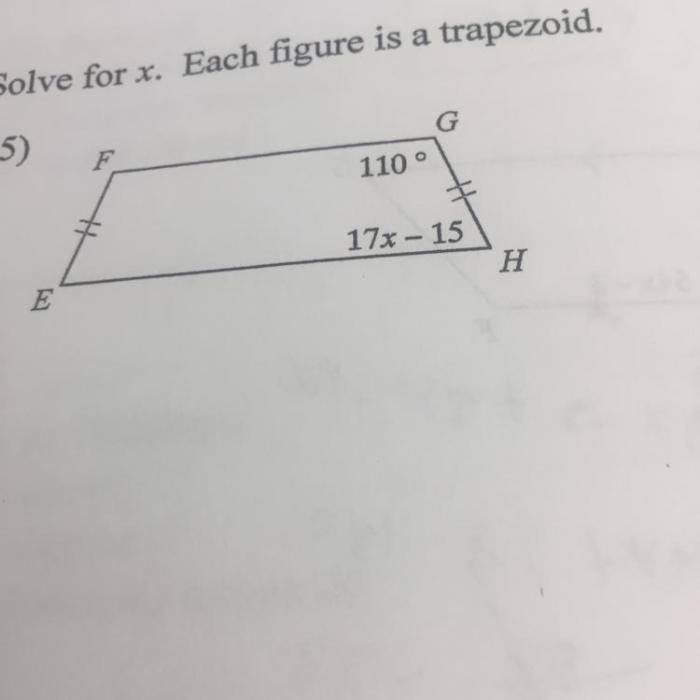
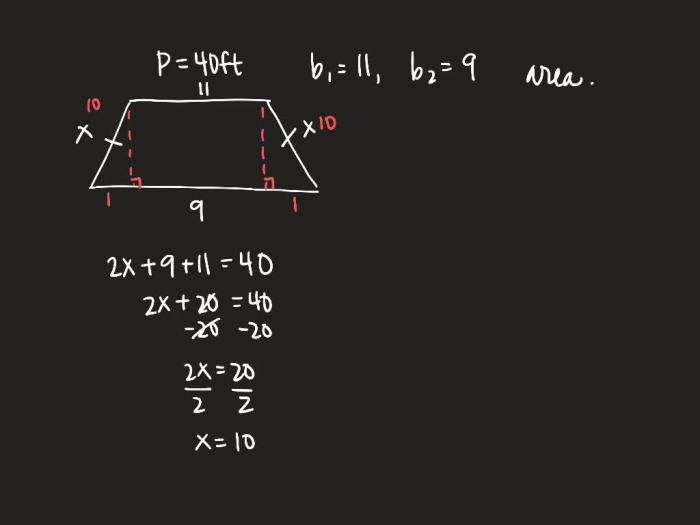Solve for x each figure is a trapezoid delves into the fascinating world of trapezoids, exploring their unique properties and providing a comprehensive guide to solving for x in these geometric shapes.
Trapezoids, with their distinct parallel bases and congruent legs, offer a rich foundation for understanding geometric concepts and their applications in real-world scenarios.
Trapezoid Basics
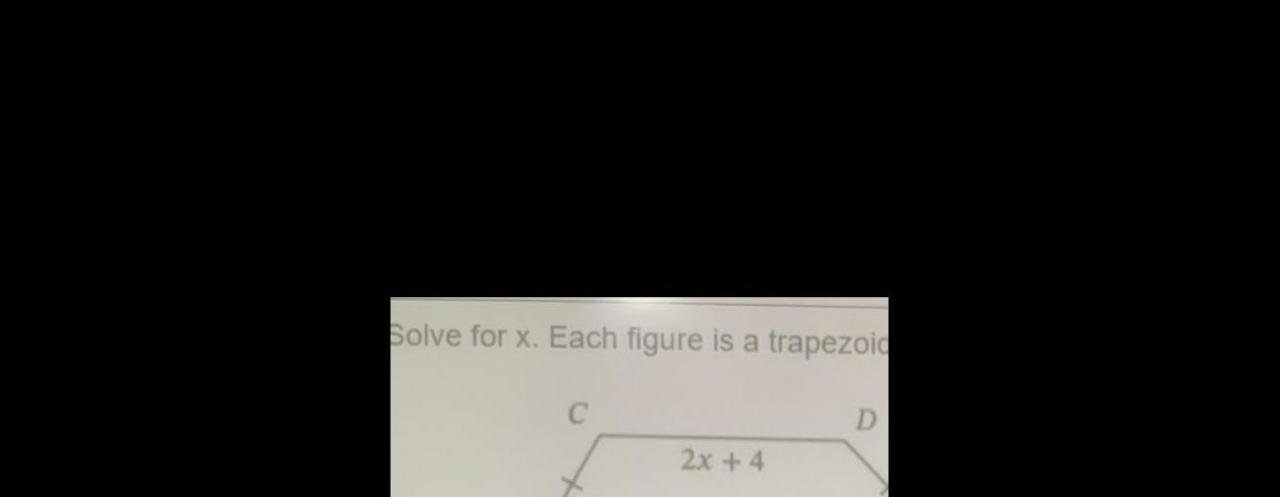
A trapezoid is a quadrilateral with two parallel sides called bases and two non-parallel sides called legs. The parallel bases are congruent, meaning they have the same length.
Properties of trapezoids include:
- Opposite angles are congruent.
- The sum of the interior angles is 360 degrees.
- The diagonals intersect at a point that divides them into congruent segments.
Solving for X in Trapezoids: Solve For X Each Figure Is A Trapezoid
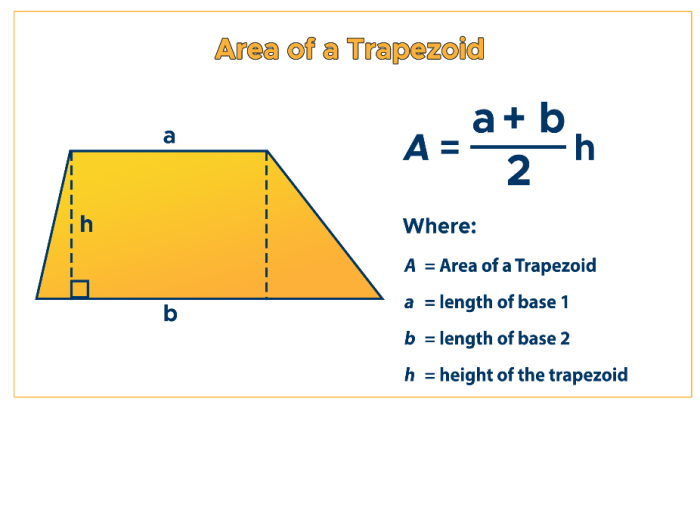
To solve for x in a trapezoid, use the formula: x = (a + b) / 2 – h
where:
- a is the length of one base
- b is the length of the other base
- h is the height of the trapezoid (the perpendicular distance between the bases)
- x is the length of the median (the line segment connecting the midpoints of the legs)
Applications of Trapezoid Formula, Solve for x each figure is a trapezoid
The trapezoid formula is used in various applications, such as:
- Calculating the area of a trapezoid
- Finding the length of a median
- Solving problems in architecture and engineering
Common Errors and Troubleshooting
Common errors when solving for x in trapezoids include:
- Using the wrong formula
- Incorrectly measuring the bases or height
- Rounding errors
To avoid these errors, carefully measure the trapezoid and use the correct formula. Double-check your calculations and round the answer to the appropriate number of significant digits.
Visual Aids
| Part | Description |
|---|---|
| Base | A parallel side of the trapezoid |
| Leg | A non-parallel side of the trapezoid |
| Height | The perpendicular distance between the bases |
| Median | The line segment connecting the midpoints of the legs |
FAQ Section
What is the formula for solving for x in trapezoids?
The formula for solving for x in trapezoids is: x = (a + b) / 2 – h, where ‘a’ and ‘b’ represent the lengths of the parallel bases, and ‘h’ represents the height of the trapezoid.
How can I apply the trapezoid formula in real-world situations?
The trapezoid formula finds applications in various fields, including architecture, engineering, and land surveying. It is used to calculate areas of trapezoidal-shaped structures, determine lengths of trapezoidal objects, and solve problems involving trapezoidal cross-sections.