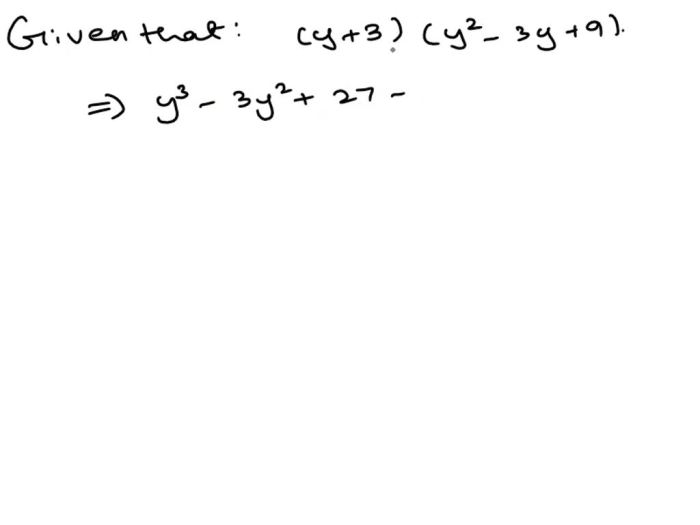Use the chart to multiply the binomial by the trinomial. – Unlock the secrets of binomial and trinomial multiplication with our comprehensive guide. Delve into the use of a multiplication chart, a powerful tool that simplifies this mathematical operation, making it a breeze for students and enthusiasts alike.
This in-depth exploration provides a clear understanding of the concepts, step-by-step instructions, and practical applications. Prepare to conquer binomial and trinomial multiplication with confidence and ease.
Binomial and Trinomial Multiplication Using a Chart: Use The Chart To Multiply The Binomial By The Trinomial.

Multiplying binomials and trinomials is a fundamental algebraic operation that involves combining two or more polynomials. This article provides a comprehensive guide to using a multiplication chart to efficiently perform binomial and trinomial multiplication.
Understanding the Concepts
A binomial is a polynomial with two terms, while a trinomial has three terms. Binomial multiplication involves multiplying the first term of one binomial by both terms of the other binomial, and then multiplying the second term of the first binomial by both terms of the second binomial.
Trinomial multiplication follows the same principle, but with an additional term to consider.
There are several methods for multiplying binomials and trinomials, including the distributive property, FOIL (First, Outer, Inner, Last), and the chart method. The chart method is a systematic approach that simplifies the multiplication process by organizing the terms in a grid.
Using the Chart, Use the chart to multiply the binomial by the trinomial.
A multiplication chart for binomials and trinomials is a grid with the terms of one polynomial listed horizontally and the terms of the other polynomial listed vertically. The product of each pair of terms is placed in the corresponding cell of the grid.
To use the chart, follow these steps:
- Set up the chart with the terms of the binomials or trinomials on the axes.
- Multiply each term in the top row by each term in the left column.
- Write the products in the corresponding cells of the grid.
- Combine like terms in each row or column to obtain the final product.
Examples and Applications
Example 1:Multiply the binomial (x + 2) by the trinomial (x 2– 3x + 5).
Using the chart method, we obtain the following grid:
| x2 | -3x | +5 | |
|---|---|---|---|
| x | x3 | -3x2 | +5x |
| +2 | 2x2 | -6x | +10 |
Combining like terms, the final product is: x3– x 2– x + 10 .
Application:Binomial and trinomial multiplication has numerous applications in various fields, such as algebra, geometry, and physics. It is used to solve equations, find the area and volume of geometric shapes, and analyze motion.
Extensions and Variations
The chart method can be extended to multiply polynomials with more than three terms. There are also variations of the chart method, such as the box method and the area model.
Alternative approaches to multiplying binomials and trinomials include using the distributive property or FOIL. Each method has its advantages and disadvantages, depending on the complexity of the polynomials involved.
Top FAQs
What is the key advantage of using a multiplication chart for binomial and trinomial multiplication?
The multiplication chart provides a systematic and organized approach, eliminating the need for memorization and reducing the risk of errors.
Can the multiplication chart method be applied to more complex polynomial expressions?
Yes, the principles of the multiplication chart can be extended to higher-order polynomials, although the process may require more steps.
What are some real-world applications of binomial and trinomial multiplication?
Binomial and trinomial multiplication find applications in various fields, including physics, engineering, and economics, where they are used to model real-world phenomena.